NLP_NaiveBayes_LogisticRegression_kNearestNeighbors
Natural Language Processing (NLP) spam/ham email classification via full custom Beta-Binomial Naive Bayes, Gaussian Naive Bayes, Logistic Regression & k-Nearest Neighbors implementation.
For usage instructions please check Usage README
For full documentation - system design, experiments & findings please read NaiveBayes_LogisticRegression_kNearestNeighborsDoc Report
Introduction
In this report I present my implementations of four pattern recognition methods: Beta-Binomial Naive Bayes, Gaussian Naive Bayes, Logistic Regression with Newton’s Method and L2 regularization learning, K-Nearest Neighbors with cross-validation, as well as, the results and analysis of the SPAM E-mail Dataset, classified with each of the above-mentioned algorithms.
The dataset is comprised of 4601 samples, each with 57 features. Out of them 1813(39.4%) are labeled as spam, leaving 2248(60.6%) as non-spam. The full description of the SPAM E-mail dataset and clarification on what is assumed as spam can be seen in [1]. The dataset is randomized and divided into two sub-sets – training with 3065 samples and a test (sometimes also used as validation) with 1536 samples. Two data-transformation techniques are applied to the training and test sets. A binarization is performed in order to prepare the dataset for the Beta-Binomial Naive Bayes fit. A log-transform is performed in order to prepare the dataset for the rest of the fits.
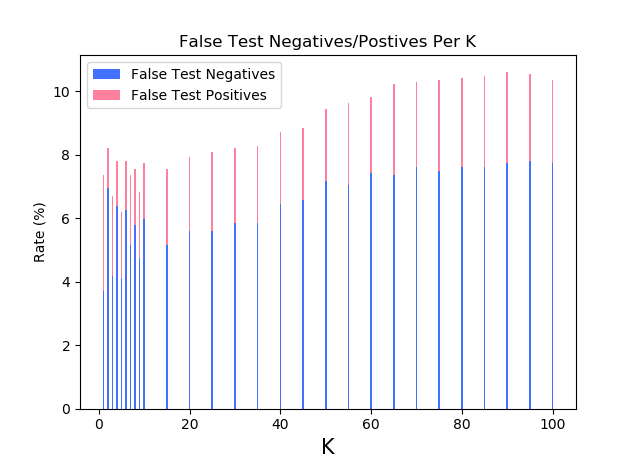
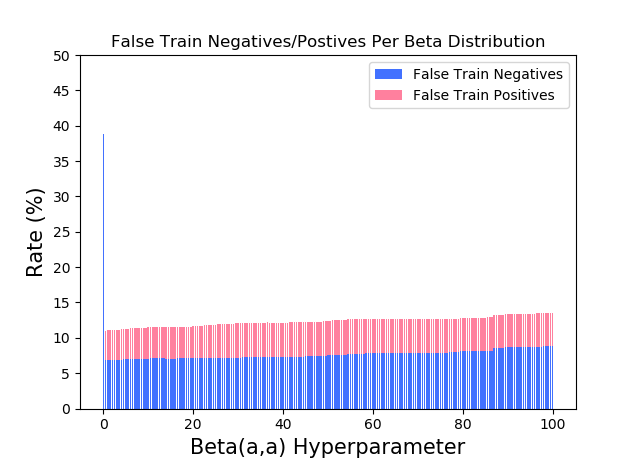
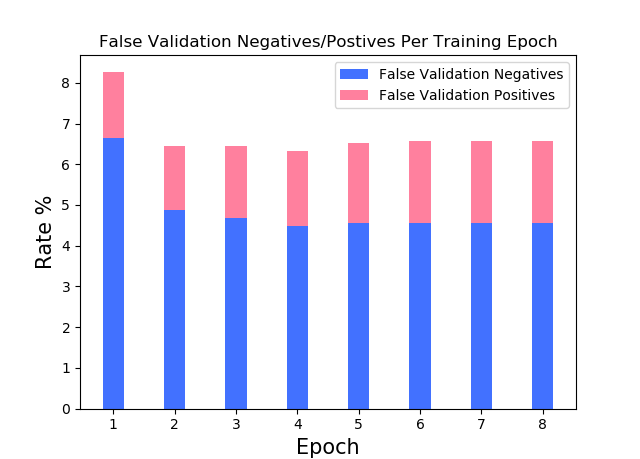
For classification analysis of the model fit, I observe a few different metrics: accuracy, overall error rate(1-accuracy), false positives error rate and false negatives error rate. While the main metrics for evaluating the performance of the methods is the resultant accuracy/overall error rate, for the specific case of the SPAM E-mail dataset – a deeper insight can be drawn from the false positives/negatives error rate. As mentioned by [1], the false positives (classifying a non-spam email as spam) is very undesirable as this can lead to the loss of important correspondence. Hence, when I discuss the performance of the model fits, a special attention is given to the false positives rate with the aim of minimizing it.
Additionally, the effect that some hyperparameters have on the model fit are studied: for the Beta(a, a)-Binomial Naive Bayes – the effect of the value of the “a” hyperparameter (hence of the prior); for the Logistic Regression method – the amplitude of the weight decay; for K-Nearest Neighbor – the value of “k”.
The four methods are implemented in Python from scratch, using NumPy for matrices manipulation and calculations. Four shared helper functions are implemented for extracting the evaluation metrics and plotting a confusion table. Further method-specific helper functions are implemented for wrapped training, testing, displaying results and complete fitting using matplotlib for plotting graphs and some other basic helper packages.
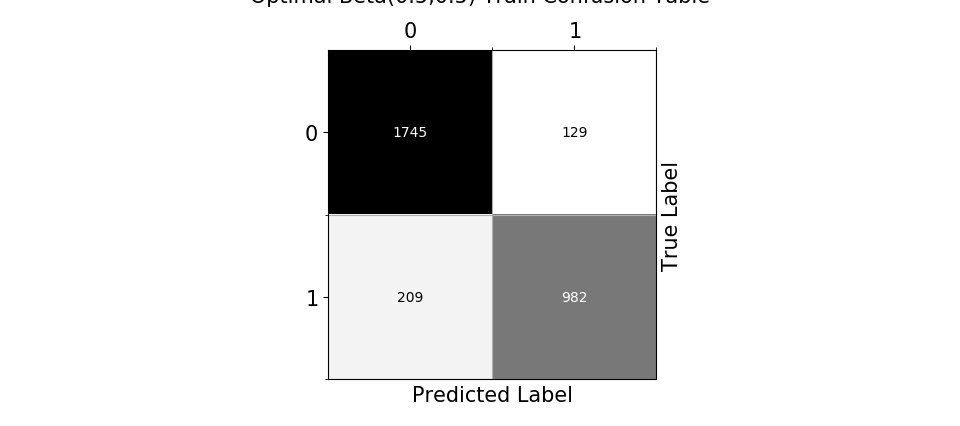
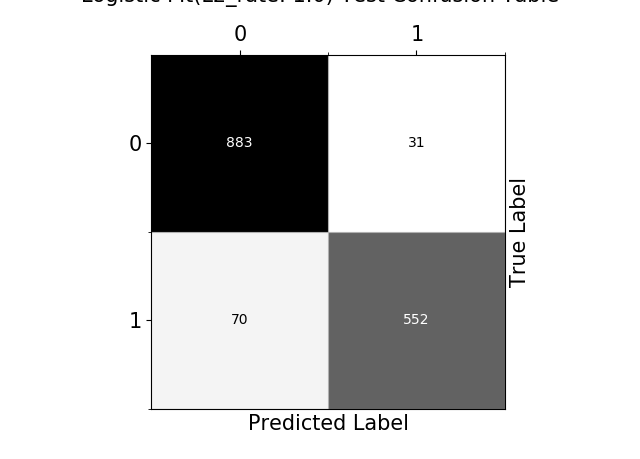
For each method graphs of {train/test} {error rate, accuracy, false negatives error rate, false positives error rate} over {(hyperparameter) fit / training(for Logistic Regression)} are plotted. Based on the train/test predictions vs targets, confusion tables are displayed. Last but not least, the optimal value for the hyperparameter at question is chosen and the corresponding best model-fit performance is displayed.
Beta-Binomial Naive Bayes Classifier
Design
The classifier is designed to be configurable to either use the Maximum Likelihood (ML) Estimation or to assume a prior Beta(a, a) (Posterior Predictive (PP)) for each – the class priors probability and the class-conditional probabilities. Depending on its configuration, the classifier can use a pure ML, a Bayesian PP or a mixture for training and prediction.
Gaussian Naive Bayes Classifier
Design
For training the classifier uses the Maximum Likelihood (ML) Estimation for the class-priors and the class-conditional mean and variance for each feature. The prediction is made by utilizing MLE as a plug-in estimator.

Logistic Regression
Design
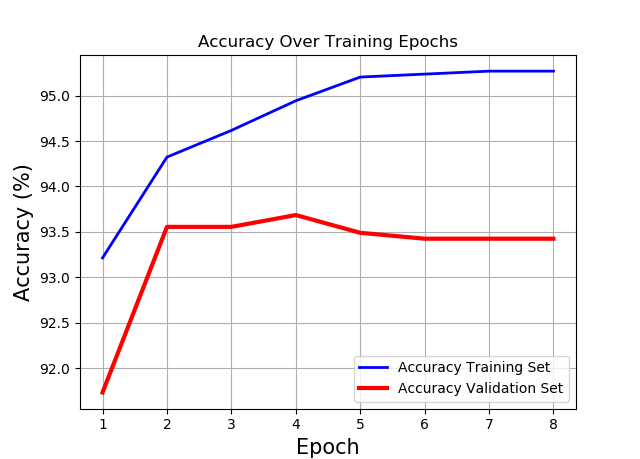
The Logistic Regression classifier is built as an artificial neuron from three layers: linear – containing the model parameters, which after a forward step yield the log-odds prediction; logistic – the sigmoid function which squashes the log-odds into [0:1] interval and yields the posterior probabilities; step – the step function with a threshold of 0.5, which translates the logistic decision boundary at 0.5 to binary predictions. The neuron learns though the Newton’s Method by doing a second order derivative cost estimation using both – the Hessian and the Gradient. The learning also utilizes a L2 regularization.
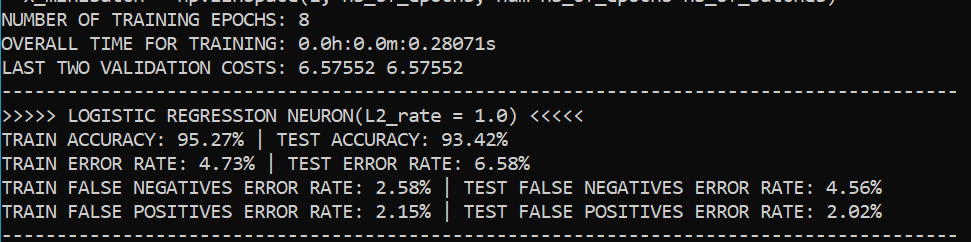
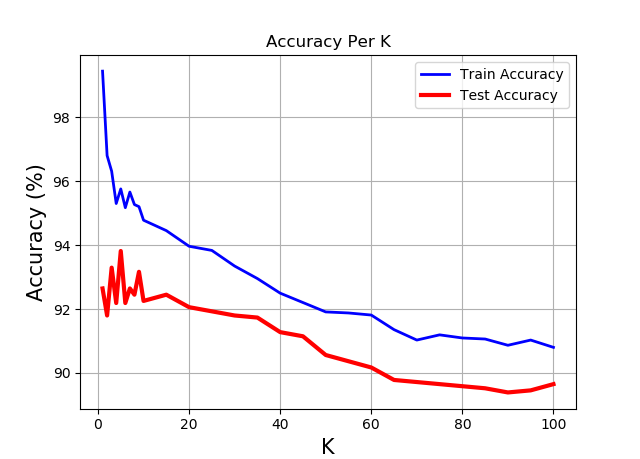
K-Nearest Neighbors
Design
The classifier measures the “nearness” between train and test samples via the Euclidean distance. The optimal K is chosen via a five-fold cross-validation.